I have been investigating search trees to see if binary search trees’ memory layout can, in practice, make a large difference in performance. Now that I’ve fixed the bugs in my test application, I can say: yes! The theory here is in so-called “cache-oblivious” algorithms. The idea is that you can use divide-and-conquer algorithms and data structures to exploit locality and ensure that at some point you will be working with the granularity of your memory transfer size (such as the size of a cache line or disk block).
How well does it work? Take a look:
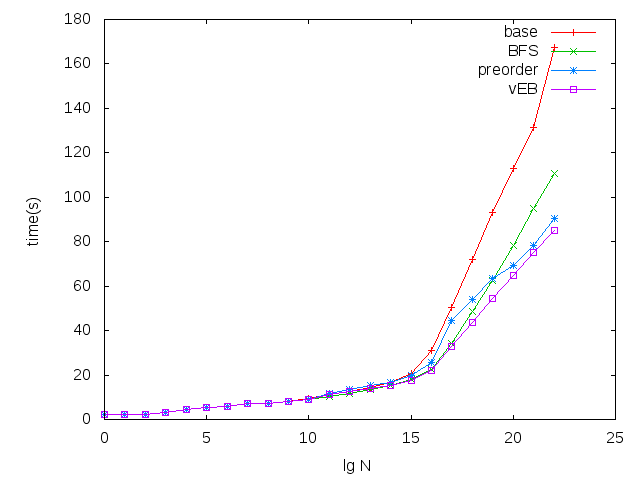
This machine has a 2 meg L2 cache and 32 K L1 d-cache. The size of nodes in this test was 32 bytes, so the L1 cache is blown at 2**10 items, and the L2 cache at 2**16.
With the exception of “base,” the trees are all laid out in an array; “vEB” is the cache-oblivious version in which the tree uses a van Emde Boas layout: the top half of the tree is stored in the array, followed by each of the subtrees in left-to-right order, recursively. Unfortunately, constructing the tree dynamically is rather complicated.
So far I’m just exploring ground that’s already been covered, but I do think this is an interesting class of data structures that hasn’t trickled out into the real world yet.
